The Net Force Calculator is an essential tool for students, engineers, and physics enthusiasts to calculate the resultant force acting on an object. By inputting up to five different forces along with their respective angles, the calculator efficiently computes the net force magnitude and direction.
This tool is invaluable in fields like mechanics, engineering, and physics education, helping users understand and apply the principles of force vector addition in real-world scenarios. Whether analyzing the forces in a mechanical system or solving complex physics problems, the Net Force Calculator offers a quick, accurate, and user-friendly solution.
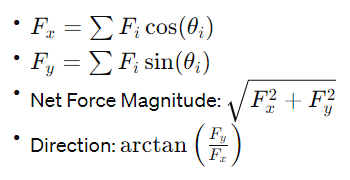
What is Net Force Calculator?
When multiple forces are applied to an object, the Net Force Calculator can be utilized to calculate its net force. Net force is defined as the sum of all forces acting in one direction on an object.
Physics treats force as a vector quantity with both magnitude and direction. Therefore, when computing the net force, both magnitude and direction must be taken into account.
Definition and Background of Net Force
Net force is the vector sum of all forces acting on an object. It determines the object’s acceleration according to Newton’s second law of motion. Understanding net force is crucial for analyzing motion in physics and engineering.
Calculating the net force acting on an object requires adding together all forces acting in one direction.
Mathematically, this can be expressed as:
Net Force (F_net) = F_1 + F_2 +… + F_n
Where F_1, F_2,…, F_n are the forces acting on an object.
However, when forces are acting in different directions we must calculate the net force for each direction separately. All forces acting in an x-direction are added up to get a net force in that direction and all those acting in y-direction add up for a net force there as well.
This can be expressed mathematically as:
Net Force in x-direction (F_net,x) = F_1x + F_2x + F_3x +…+F_nx.
Net Force in Y-direction (F_net,y) = F_1y + F_2y + F_3y +…+F_ny
F_1x, F_2x, F_3x…, and F_nx are the forces acting on an object in the x-direction; while F_1y, F_2y, F_3y..,and F_ny are its counterparts in the y-direction.
Once we have calculated the net force in both directions, we can use Pythagorean theorem to calculate its magnitude and inverse tangent function to determine force angle.
The Pythagorean theorem can be expressed mathematically as:
Net Force Magnitude = (F_net,x2 + F_net,y2)
The force angle (th) can be calculated using the inverse tangent function as follows:
Force Angle (th) = tan-1(F_net,y / F_net,x).
To use the Net Force Calculator, enter all force values and angles applied to an object. After entering all your values, click “Calculate” for a net force magnitude, angle, as well as its x and y components.
Consider an object being pulled at 30 degrees, 60 degrees and 90 degrees angles on a frictionless surface by three forces: 10 N, 20 N and 30 N. To calculate its net force effect on this object, each force must first be broken down into its x and y components before adding them together to calculate its total effect.
The x-component of a 10 N force is 10cos(30deg) = 8.66 N, while its y component is 10sin(30deg).
The 20 N force has two components, 20cos(60deg) = 10 N and y-component 20sin(60deg).
3.32 N.
The x-component of this 30 N force is 30cos(90deg) = 0 N, while its y component is 30sin(90deg).
30 N.
The net force in the x-direction is equal to the sum of all forces acting along its x axis: 8.66 N + 10 N + 0 N
= 18.66 N.
The total net force in the y-direction is equal to the sum of all components of these forces: 5 N + 17.32 N + 30 N
= 52.32 N.
By Pythagorean theorem, the net force magnitude is equal to 55 N because (18.662 + 52.322)
= 55 N.
The force angle is calculated using the inverse tangent function: tan-1(52.32 N / 18.66 N)
= 71.4 deg.
The Net Force Calculator indicates that the net force acting on an object is 55 N at 71.4 degrees angle. This calculation demonstrates how to accurately determine the total sum of all forces acting simultaneously on an object using a Net Force Calculator.
Net Force Calculators are invaluable tools for physics students and professionals, helping to calculate the net force applied to an object when multiple forces are applied.
By inputting magnitude and angle of inputted forces, this calculator quickly calculates their combined effect: net force magnitude, angle, as well as its x and y components – saving time by eliminating errors that could occur manually when doing it by hand.
Step-by-Step Calculation Guide for Net Force
- Identify Individual Forces: List all forces acting on the object, along with their directions.
- Input Data: Enter each force’s magnitude and angle into the calculator.
- Calculate and Interpret: Use the calculator to find the net force and its direction, which determines the object’s motion.
Table of Example Calculations for Net Force
| Force 1 (N) | Angle 1 (degrees) | Force 2 (N) | Angle 2 (degrees) | Net Force (N) | Direction (degrees) |
|---|---|---|---|---|---|
| 10 | 0 | 5 | 90 | 11.18 | 26.57 |
| 20 | 45 | 10 | 180 | 17.07 | 112.62 |
| 15 | 30 | 10 | 270 | 17.92 | 326.31 |
Glossary for Net Force Calculator Calculations
- Vector: A quantity with both magnitude and direction.
- Magnitude: The size or length of a vector.
- Newton’s Second Law: States that the acceleration of an object is proportional to the net force acting on it and inversely proportional to its mass.
FAQ Section for Net Force Calculator
Q: How does angle affect net force calculation? A: The angle determines the direction of the force vector, affecting the net force’s direction and magnitude.
Q: Can net force be zero? A: Yes, if forces are balanced, resulting in no acceleration.
Q: Is net force applicable in real-world scenarios? A: Absolutely, it’s fundamental in engineering, physics, and understanding everyday phenomena like motion and equilibrium.

