The Central Limit Theorem Calculator is a crucial tool for statisticians, data analysts, and researchers, simplifying complex statistical calculations. By entering the population mean, population standard deviation, and sample size, this calculator efficiently computes the sample standard deviation, a key measure in statistical analysis.
Central Limit Theorem Calculator – Instantly Estimate Sampling Distribution Properties
Our team converts drinks into code — fuel us to build more free tools!
Moreover, Central Limit Theorem Calculator allows for the calculation of the population standard deviation and sample size, given the other two values. This capability makes it an invaluable resource in fields such as sociology, economics, and psychology, where understanding sample behavior relative to the larger population is fundamental.
How to Use the Central Limit Theorem Calculator
Using the Central Limit Theorem Calculator is intuitive and efficient. Begin by entering the population mean (the average value of the entire population), the population standard deviation (a measure of the spread of values in the population), and the sample size (the number of observations in your sample).
After entering these values, click on the ‘Calculate Sample Std. Dev.’ button. The calculator will then compute the sample standard deviation and display the result. If you wish to conduct a new calculation, simply use the ‘Reset’ button to clear all inputs.
Explaining the Central Limit Theorem Formula
The formula utilized in the Central Limit Theorem Calculator for calculating the sample standard deviation is:
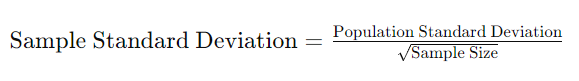
This formula is integral to the central limit theorem, which states that, given a sufficiently large sample size, the distribution of the sample means will approximate a normal distribution, regardless of the population’s distribution. The denominator, the square root of the sample size, scales the population standard deviation to the sample level. This scaling is crucial in understanding how much variability one can expect in sample means from the population mean.
Step-by-Step Calculation Guide
Let’s illustrate how to use the Central Limit Theorem Calculator with an example:
- Population Mean (μ): Assume a population mean of 100.
- Population Standard Deviation (σ): Let’s say the population standard deviation is 20.
- Sample Size (n): Consider a sample size of 50.
Input these values into the calculator:
- Population Mean = 100
- Population Standard Deviation = 20
- Sample Size = 50
Click ‘Calculate Sample Std. Dev.’. The calculator will perform the computation, displaying the sample standard deviation.
Definition and Background of the Central Limit Theorem
The central limit theorem is a fundamental principle in probability theory and statistics. It postulates that for a large enough sample size, the sampling distribution of the sample mean will be approximately normally distributed, regardless of the population’s distribution. This theorem is essential because it justifies the use of normal probability distributions in many statistical methods, even when the underlying population distribution is not normal.
The theorem has widespread applications, from quality control in manufacturing to polling in political science. It forms the basis for the creation of confidence intervals and is crucial in hypothesis testing, where the normality of distributions is often assumed. The central limit theorem is especially significant in fields like finance and economics, where it’s used to model stock prices, risk assessments, and other key metrics.
Table of Example Calculations for Central Limit Theorem
Below is a table with different scenarios illustrating the application of the central limit theorem. Each scenario includes values for population mean, population standard deviation, and sample size, along with the calculated sample standard deviation.
| Population Mean | Population Std. Dev. | Sample Size | Sample Std. Dev. |
|---|---|---|---|
| 100 | 20 | 50 | 2.83 |
| 80 | 15 | 40 | 2.37 |
| 120 | 25 | 30 | 4.58 |
| 150 | 30 | 60 | 3.87 |
| 90 | 18 | 45 | 2.68 |
In the first scenario, a population mean of 100, with a population standard deviation of 20 and a sample size of 50, results in a sample standard deviation of 2.83. This smaller sample standard deviation indicates how the variability of sample means around the population mean decreases as the sample size increases.
Glossary for Central Limit Theorem
- Central Limit Theorem: A statistical theory stating that the distribution of sample means approximates a normal distribution for large sample sizes, regardless of the population’s distribution.
- Population Mean (μ): The average value of a population.
- Population Standard Deviation (σ): A measure of the spread of values in a population.
- Sample Size (n): The number of observations in a sample.
- Sample Standard Deviation: A measure of the spread of sample means around the population mean.
FAQ Section:
- What is the Central Limit Theorem Calculator primarily used for? The Central Limit Theorem Calculator is used to calculate the sample standard deviation, helping to understand the spread of sample means around the population mean.
- Why is the Central Limit Theorem important in statistics? The Central Limit Theorem is crucial as it allows statisticians to use normal probability distributions for hypothesis testing and confidence intervals, even when the population distribution is unknown or not normal.
- Can the Central Limit Theorem Calculator determine the population mean? The calculator focuses on the sample standard deviation. However, knowing the population mean is essential for input to get accurate results.
- How large should the sample size be for the Central Limit Theorem to apply? While there’s no fixed rule, a sample size of 30 or more is generally considered sufficient for the central limit theorem to hold true.
- Is the Central Limit Theorem applicable only to normal distributions? No, one of the key aspects of the central limit theorem is that it applies regardless of the population’s distribution, assuming the sample size is large enough.
This comprehensive understanding of the Central Limit Theorem Calculator not only enhances the accuracy of statistical analyses but also empowers users across various fields to make more informed decisions based on robust statistical evidence.
Additional Online Resources about Central Limit Theorem Calculator
Here’s an overview of Additional Online Resources about Central Limit Theorem Calculator along with their hyperlinks:
- Scribbr: Central Limit Theorem: This source provides a detailed explanation of the Central Limit Theorem, emphasizing its fundamental importance in statistics. It includes examples using both continuous and discrete distributions, helping readers understand how the theorem applies in various contexts. The site explains the theorem with practical examples, making it easier to grasp for those new to the concept.
- Statistics By Jim: Central Limit Theorem Explained: This resource focuses on the practical applications and significance of the Central Limit Theorem. It uses simple experiments like dice rolls and coin flips to illustrate the theorem’s effect on different sample sizes. The website also discusses the normality assumption in statistics and the impact of sample size on the precision of estimates.
- Statistics How To: Central Limit Theorem: Definition and Examples: This site offers a step-by-step approach to understanding and applying the Central Limit Theorem. It provides a clear guide on calculating and interpreting z-scores, along with specific examples. This is a great resource for beginners who need a structured approach to learning about the theorem.
- Wikipedia: Central Limit Theorem: The Wikipedia page gives a theoretical and historical view of the Central Limit Theorem. It covers the earliest forms of the theorem and its evolution, including various versions like the de Moivre–Laplace theorem. This source is ideal for those interested in the mathematical foundations and historical development of the theorem.



