The Endpoint Calculator is an essential tool for mathematicians, engineers, architects, and anyone involved in fields requiring linear equation solutions. By inputting the slope of a line, the y-intercept (constant b), and either the x or y coordinate of an endpoint, this calculator efficiently computes the missing coordinate.
Endpoint Calculator – Instantly Find the Endpoint of a Line Segment
Using Endpoint Calculator simplifies tasks such as plotting linear equations, designing structures, and solving geometry problems, making it a valuable resource in various applications.
How to Use the Endpoint Calculator
- Enter the Slope (m): Input the slope of the line.
- Input the Constant b: Provide the y-intercept value of the line.
- Provide the X or Y Coordinate: Enter either the x or y coordinate of the endpoint.
- Calculate: Click the ‘Calculate’ button to find the missing coordinate.
- Reset: Use the ‘Reset’ button to clear the fields for a new calculation.
Understanding the Calculation Method
The Endpoint Calculator uses the linear equation:
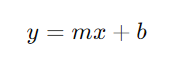
Where:
- m is the slope of the line.
- b is the y-intercept (constant b).
- x and y are the coordinates of a point on the line.
If x is provided, the calculator finds y, and if y is provided, it calculates x.
Endpoint Calculator: Definition and Importance
An Endpoint Calculator is a tool used to determine a missing coordinate on a linear equation. This is crucial for accurately plotting lines on graphs, solving geometric problems, and understanding spatial relationships in various fields.
Step-by-Step Calculation Guide
- Enter Slope: For example, 2.
- Provide Constant b: Say, 3.
- Enter X or Y Coordinate: Assume x = 5.
- Calculate: The calculator will display y = 13.
Examples of Endpoint Calculations
| Slope | Constant b | X Coordinate | Y Coordinate | Missing Coordinate |
|---|---|---|---|---|
| 2 | 3 | 5 | – | y = 13 |
| -1 | 4 | – | 7 | x = 1 |
| 0.5 | 2 | 10 | – | y = 7 |
Alright, let’s delve into this table and understand it from a mathematical perspective, suitable for a classroom setting.
Imagine we’re dealing with a fundamental concept in algebra and coordinate geometry: the equation of a straight line, which is typically written as y = mx + b. Here, m represents the slope of the line, and b is the y-intercept, the point where the line crosses the y-axis.
Now, let’s analyze the table you’ve provided in this context:
Understanding Slope (m) and Y-Intercept (b):
- The slope,
m, indicates the steepness and direction of the line. A positive slope means the line inclines upwards, while a negative slope indicates it declines downwards as we move from left to right. A slope of zero implies a horizontal line. - The y-intercept,
b, is where the line crosses the y-axis. It’s the value ofywhenxis zero.
Solving for Missing Coordinates:
- In each case, we’re given enough information to determine the missing coordinate using the linear equation.
First Example (Row 1):
- Given: Slope (
m) = 2, Constant (b) = 3, X Coordinate = 5, Y Coordinate = missing. - To find Y, we plug the values into the equation
y = mx + b. So,y = 2 * 5 + 3 = 13. - Interpretation: When
xis 5,yis 13 on this particular line.
Second Example (Row 2):
- Given: Slope (
m) = -1, Constant (b) = 4, X Coordinate = missing, Y Coordinate = 7. - We need to rearrange the formula to solve for
x:x = (y - b) / m. Thus,x = (7 - 4) / -1 = 1. - Interpretation: When
yis 7,xis 1 on this line. The negative slope indicates the line is declining.
Third Example (Row 3):
- Given: Slope (
m) = 0.5, Constant (b) = 2, X Coordinate = 10, Y Coordinate = missing. - Applying
y = mx + b, we gety = 0.5 * 10 + 2 = 7. - Interpretation: At
xequals 10, theyvalue is 7. This line is rising, but not as steeply as the first one (since 0.5 < 2).
This exercise is a practical application of how to use the linear equation in finding missing coordinates. It demonstrates the relationship between the slope, a point on the line, and how these elements define the position and direction of a line on a Cartesian plane. Remember, the beauty of algebra lies in its ability to let us explore and solve such geometrical puzzles with elegant simplicity.
Glossary for Endpoint Calculator
- Slope (m): The rate at which the line inclines or declines.
- Constant b: The y-intercept, where the line crosses the y-axis.
- Endpoint: A point at the end of a segment or line.
FAQ Section
Q: Can this calculator be used for vertical lines?
A: No, as vertical lines have an undefined slope, this calculator is not suitable for such cases.
Q: Is it possible to calculate the endpoint if both x and y are given?
A: The calculator is designed to find the missing coordinate when either x or y is given, not both.
Q: How important is accuracy in the slope and constant b values?
A: Accuracy is crucial as even slight variations can significantly change the location of the endpoint on a line.
The Endpoint Calculator is a valuable tool for anyone dealing with linear equations, providing a quick and efficient way to determine missing coordinates and enhancing understanding of linear relationships.
Additional Useful Online Resources about Endpoint Calculator
For anyone looking to enhance their understanding of algebra and coordinate geometry, here are some excellent online resources:
- Khan Academy – Geometry and Analytic Geometry: Khan Academy offers comprehensive lessons on various topics in geometry, including analytic geometry. This resource is particularly beneficial for its structured approach to learning, with units covering everything from the basics of geometry to more complex concepts in analytic geometry. It includes interactive exercises, quizzes, and instructional videos, making it a great tool for both students and educators. Visit Khan Academy’s geometry section at Khan Academy – Geometry.
- Math Open Reference – Introduction to Coordinate Geometry: Math Open Reference provides an accessible introduction to coordinate geometry. It’s an excellent starting point for beginners, explaining the basics of the coordinate plane, the concept of coordinates, and their application in geometry. The site also delves into the history of coordinate geometry and offers insights into other related topics. You can explore this resource at Math Open Reference.
- Purplemath: Purplemath offers clear and practical lessons in algebra, tailored for students who might find mathematical concepts challenging. The lessons are designed to be student-friendly, focusing on practical techniques, common pitfalls, and helpful strategies. It’s an excellent resource for homework help and clarifying algebra concepts. Check out the lessons at Purplemath.
- Desmos: Desmos is an advanced online graphing calculator ideal for plotting functions, creating tables, and exploring transformations. It’s a very interactive and user-friendly tool that can greatly aid in understanding and visualizing algebraic and geometric concepts. Visit Desmos at Desmos.
These resources provide a blend of theoretical knowledge and practical tools to help learners grasp the essentials of algebra and coordinate geometry effectively.



