The Unit Circle Calculator is a tool designed to simplify the process of understanding trigonometric functions. Ideal for students, educators, and anyone with an interest in mathematics, this calculator allows users to input an angle of the unit circle, instantly displaying the corresponding sine, cosine, and tangent values.
Sine:
Cosine:
Tangent:
This functionality is crucial for visualizing and comprehending the relationships between angles and trigonometric ratios, thus enhancing the learning and problem-solving experience in trigonometry.
How to Use the Unit Circle Calculator
To use the Unit Circle Calculator, follow these simple steps:
- Enter the Angle: Type the angle (in degrees) into the provided input field.
- Calculate: Click the ‘Calculate’ button to compute the trigonometric functions.
- View Results: The sine, cosine, and tangent values will be displayed in the results area.
- Reset: To perform a new calculation, click the ‘Reset’ button to clear all fields.
Unit Circle Calculator and Its Formulas
The unit circle is a fundamental concept in trigonometry. It’s a circle with a radius of one unit, centered at the origin of a coordinate system. The sine, cosine, and tangent of an angle are the y-coordinate, x-coordinate, and y-coordinate divided by x-coordinate of the point on the unit circle that corresponds to that angle, respectively.
- Sine (sin):
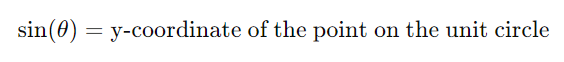
- Cosine (cos):
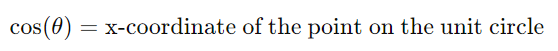
- Tangent (tan):
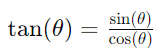
Background of the Unit Circle
The unit circle is a cornerstone in the study of trigonometry and circular functions. Its origin dates back to ancient civilizations, where it was used to study astronomical patterns and seasons. Today, it plays a crucial role in various fields such as physics, engineering, and computer science.
Step-by-Step Calculation Guide
Let’s use the Unit Circle Calculator for an example angle of 45 degrees:
- Enter 45 in the angle input field.
- Click Calculate to obtain the results.
- Observe the calculated values of sine (0.7071), cosine (0.7071), and tangent (1.0000).
Examples of Calculations
Alright, let’s explain Unit Circle Calculator calculations and formulas with this table in more depth:
| Angle (Degrees) | Sine Value | Cosine Value | Tangent Value |
|---|---|---|---|
| 30 | 0.5000 | 0.8660 | 0.5774 |
| 45 | 0.7071 | 0.7071 | 1.0000 |
| 60 | 0.8660 | 0.5000 | 1.7321 |
This table is about trigonometric functions – specifically, sine, cosine, and tangent – and their values for specific angles. Let’s break down each column:
Angle (Degrees):
This column lists angles in degrees. In trigonometry, angles are a fundamental concept. We are looking at three specific angles here: 30 degrees, 45 degrees, and 60 degrees. These angles are commonly used in trigonometry because they are part of a special group of triangles known as right-angled triangles, specifically those that are half of an equilateral triangle (30° and 60°) or isosceles right-angled triangles (45°).
Sine Value:
The sine of an angle in a right triangle is a ratio. It is the length of the side opposite the angle divided by the length of the hypotenuse (the longest side of the triangle, opposite the right angle). For example, at 30 degrees, the sine value is 0.5000. This means if you have a right triangle with a 30-degree angle, the ratio of the length of the side opposite to this angle to the hypotenuse is 0.5.
Cosine Value:
Cosine is another trigonometric function, similar to sine but instead considers the adjacent side to the angle. Cosine of an angle in a right triangle is the ratio of the length of the adjacent side to the angle, to the hypotenuse. For instance, at 45 degrees, the cosine value is 0.7071, indicating that the length of the side adjacent to the 45-degree angle is about 0.7071 times the length of the hypotenuse.
Tangent Value:
Tangent is the third trigonometric function shown here. It’s defined as the ratio of the sine of an angle to the cosine of that angle. In terms of triangle sides, it’s the ratio of the opposite side to the adjacent side. For the 60 degrees angle, the tangent value is 1.7321, which means the opposite side is 1.7321 times longer than the adjacent side.
The values in this table are rounded to four decimal places. These specific values are quite important and are often memorized in trigonometry because they can help solve various problems related to angles and triangles, especially in right triangles.
It’s also important to note that these functions are periodic, meaning they repeat their values in a regular pattern, and they are related to the unit circle, where the angle is measured from the positive x-axis in an anti-clockwise direction.
By understanding these concepts, students can solve a wide range of problems in geometry, physics, engineering, and other fields that involve measuring angles and calculating distances or heights.
Glossary for the Unit Circle
- Unit Circle: A circle with a radius of one unit.
- Radians: A unit of angular measure used in trigonometry.
- Sine (sin): A trigonometric function representing the y-coordinate on the unit circle.
- Cosine (cos): A trigonometric function representing the x-coordinate on the unit circle.
- Tangent (tan): A trigonometric function representing the ratio of sine to cosine.
FAQ Section
Q: What is the unit circle? A: The unit circle is a circle with a radius of one unit, used to define trigonometric functions.
Q: Why are radians used in the calculator? A: Radians provide a direct relationship between the angle and the length of the arc on the unit circle, making calculations more straightforward.
Q: Can the calculator handle angles greater than 360 degrees? A: Yes, the calculator can handle any angle, as trigonometric functions are periodic.
Q: How accurate are the calculator’s results? A: The calculator provides results accurate to four decimal places, which is sufficient for most applications.
This Unit Circle Calculator serves as an essential tool for exploring and understanding the fascinating world of trigonometry, offering immediate insights into the trigonometric values of any angle.
Additional Reading Material about Unit Circle Calculator
If you’re interested in learning more about trigonometry, there are several online resources that offer comprehensive lessons and practice exercises:
- Khan Academy: Khan Academy provides a detailed course on trigonometry, covering topics like right triangles, trigonometric functions, non-right triangles, and trigonometric equations and identities. It’s a great resource for beginners as well as for those looking to brush up on their skills. The course is structured into units and includes various interactive problems and quizzes to test your understanding. Khan Academy Trigonometry
- Brilliant: Brilliant offers a course in trigonometry that focuses on mastering the fundamentals, including the definitions of trigonometric functions and solving triangles. The course is interactive and includes challenging problems and animated graphs. It’s suitable for those who prefer learning through problem-solving and application. Brilliant Trigonometry Course
- Math is Fun: This website provides a more casual approach to learning trigonometry. It explains the basics like sine, cosine, and tangent, and includes examples to illustrate how these functions are used in practical scenarios, such as calculating heights and distances. It’s a great resource for quick reference and easy-to-understand explanations. Math is Fun – Trigonometry
- School Yourself: This site offers lessons on various aspects of trigonometry, such as radians, trig functions, special angles, the unit circle, and inverse trig functions. It also covers more advanced topics like trig identities and triangle formulas. The content is well-organized, making it easy to navigate through different topics. School Yourself – Trigonometry
These resources cater to a range of learning styles and provide a thorough understanding of trigonometry, from basic concepts to more advanced topics. Whether you’re a complete beginner or looking to deepen your understanding, these platforms can be very helpful.

